Los ángulos, como ya se ha vistos, son porciones de espacio encerradas entre dos líneas (lados del ángulo) que se cortan en un punto llamado vértice. Los ángulos permiten que se hagan una serie de operaciones con ellos.
A continuación veremos cómo se realizan las operaciones siguientes:
- Transladar o transportar un ángulo A de un lugar a otro.
- Suma de ángulos. Sumar los ángulos A, B y C.
- Restar al ángulo mayor A , el ángulo menor B.
- Multiplicar un ángulo por un número. Multiplicar el ángulo A x 3.
- Dividir un ángulo en dos partes iguales. BISECTRIZ.
- Trazado de bisectrices especiales:
- Trazado de la bisectriz de un ángulo cuando el vértice queda fuera de los límites del dibujo.
- Trazar una recta que pase por un punto P dado y que sea concurrente con otras dos (rectas r y s).
- Bisectriz de un ángulo curvilíneo
- Bisectriz de un ángulo mixtilíneo

2.1.1. Transladar o transportar un ángulo.
Las operaciones con ángulos se basan en poder trasladar un ángulo de un lugar a otro. Por este motivo, la operación de transportar un ángulo es muy importante.
En este apartado veremos cómo trasladar un ángulo de un sitio a otro. Existen varias formas de hacer esta operación, incluso utilizando un transportador de ángulo. Con el transportador de ángulos, tendríamos que medir el ángulo y construir el mismo ángulo en el sitio que nos pidan.
En este caso, veremos cómo se resuelve gráficamente este problema, es decir, utilizando una regla y un compás.
 OPERACIONES
OPERACIONES
- Nos dan cómo dato el ángulo A y nos piden que traslademos el ángulo sobre la recta r y a partir del punto A’.
- Cogiendo un compás, pinchamos sobre el vértice A y abrimos el compás con una medida cualquiera. Trazamos un arco que corte los dos lados del ángulo. Obtenemos los puntos 1 y 2.
- Con la misma abertura del compás utilizada para la operación anterior, se traza otro arco en el punto A’. El arco trazado corta a la recta r en el punto 1′.
- Utilizando el compás, cogemos la distancia que hay entre 1 y 2. Pinchamos en 1 y abrimos el compás hasta 2. Con esta medida del compás, vamos al punto 1′ y trazamos un arco sobre el arco que teníamos. Obtenemos el punto 2′.
- Unimos el vértice A’ y el punto 2′ y tendremos el ángulo transportado.
.
2.1.2. Suma de ángulos.
Conociendo bien la operación anterior, las siguientes seon muy sencillas. Para sumar ángulos, tan solo habrá que trasladar los ángulos uno a continuación de otro.
En este caso, nos piden sumar los ángulos A, B y C

OPERACIONES:
- Nos dan como dato los ángulos A, B y C, y nos piden que los sumemos a partir de un punto O que está situado en la recta r.
- Deberemos trasladar los ángulos, uno a continuación del otro, partiendo del primero (ángulo A).
- Con una abertura cualquiera del compás, se traza un arco en los ángulos A, B y C. También, con la misma abertura, trazamos otro arco en el punto O.
- Obtenemos unos puntos que me servirán de ayuda para la realización de la suma que nos piden. Estos puntos son: en el A, tendremos 1 y 2; en el B, tendremos 3 y 4 y en el C, tendremos 5 y 6. Además, en la recta r y con el punto O, tendré el punto 1′.
- Se toman las medidas de cada uno de los ángulos. Con el compas, cogemos la abertura que tiene el ángulo A. Pinchamos en 1 y abrimos el compás hasta 2.
- Con esta abertura del compás, vamos al punto 1′ y trazamos un arco. Obtenemos el punto 2′.
- Repetimos los pasos 5 y 6 para los ángulos B y C. Obtenemos los puntos 4′ y 6′.
- Si unimos la recta r hasta el punto O, y este con 6′, tenemos el ángulo suma A+B+C. Si unimos los puntos 2′, 4′ y 6′ con O tendremos los ángulos originales A, B y C trasladados a este punto para hayar la suma.
.
2.1.3. Restar al ángulo A el ángulo B.
Se trata de la misma forma que la suma, pero en vez de llevar el ángulo a «continuación», se lleva «hacia atrás». Las operaciones, por tanto, son similares a las de la suma. Habrá que tener en cuenta que el segundo ángulo habrá que llevarlo hacia atrás, hacia el inicio.
OPERACIONES
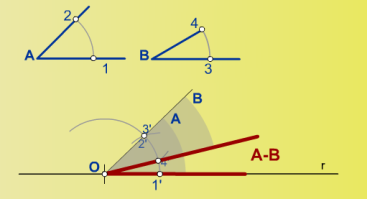
- Nos dan como dato los ángulos A y B, y nos piden que hayemos la diferencia, es decir, que al mayor (ángulo A) le quitemos el menor (ángulo B) y veamos cual es el resultado. Nos piden que lo hagamos a partir de un punto O que está situado en la recta r.
- Deberemos trasladar el ángulo A. Con una abertura cualquiera del compás, se traza un arco en los ángulos A y B. También, con la misma abertura, trazamos otro arco en el punto O.
- Obtenemos unos puntos que me servirán de ayuda para la realización de la suma que nos piden. Estos puntos son: en el A, tendremos 1 y 2; en el B, tendremos 3 y 4. Además, en la recta r y con el punto O, tendré el punto 1′.
- Con el compas, cogemos la abertura que tiene el ángulo A. Pinchamos en 1 y abrimos el compás hasta 2.
- Con esta abertura del compás, vamos al punto 1′ y trazamos un arco. Obtenemos el punto 2′.
- Cogemos la abertura del ángulo B y lo llevamos a partir de 2′, pero en vez de hacerlo a continuación del que habíamos construido, lo hacemos hacia atras, volviendo hacia el 1′. Tenemos el punto 4′.
- El ángulo resta (A-B) será el formado por la recta r, vertice O y el lado formado por 4′ y O.
.
2.1.4. Multiplicar un ángulo por un número.
De la misma forma que pasaba con los segmentos, no podemos multiplicar un ángulo por otro ángulo. Pero SÍ que se puede multiplicar un ángulo por un número cualquiera. La solución es secilla, porque se trata de sumar el ángulo tantas veces como nos lo indique el multiplicador.
En este ejercicio nos piden multiplicar el ángulo A por 3. Visto lo anterior, tendremos que sumar tres veces el ángulo A.

OPERACIONES
- Nos dan como dato el ángulo A y nos piden que lo multipliquemos por 3. Igual que en los casos anteriores, lo haremos a partir de un punto O que está situado en la recta r.
- Deberemos trasladar el ángulo A. Con una abertura cualquiera del compás, se traza un arco en los ángulo A. También, con la misma abertura, trazamos otro arco en el punto O.
- En el ángulo A obtenemos unos puntos que me servirán de ayuda para la realización del ejercicio. Son los puntos 1 y 2. Mientras que en la recta r, tendré el punto 1′.
- Con el compas, cogemos la abertura que tiene el ángulo A. Pinchamos en 1 y abrimos el compás hasta 2.
- Con esta abertura del compás, vamos al punto 1′ y trazamos TRES arcos, uno a continuación del otro. Obtenemos el punto 2′.
- El ángulo resultante (Ax3) será el formado por la recta r, vertice O y el lado formado por 2′ y O.
.
2.1.5. Dividir un ángulo en dos partes iguales. BISECTRIZ.
La bisectriz es la línea que divide el ángulo en dos partes iguales. Esta propiedad hace que el trazado de la bisectriz sea muy importante.
Nos plantean el siguiente ejercicio: nos dan el ángulo A y nos piden dividirlo en 2 partes iguales, es decir, nos piden trazar la bisectriz del ángulo A

OPERACIONES.
- Pinchando con el compás en el vértice del ángulo A y abriendo el compás la medida que se quiera, se traza un arco que corta a los lados del ángulo en los puntos 1 y 2.
- Ahora cogemos una abertura del compás, algo superior a la mitad del arco 1-2. La abertura puede ser cualquiera pero tiene que ser algo mayor al citado arco.
- Con esta abertura se trazar un arco desde 1 y otro desde 2. Se cortan en el punto 3.
- Uniendo 3 con el vértice del ángulo A, obtenemos la BISECTRIZ.
Estas son las operaciones para dividir un ángulo en dos partes iguales, pero no hay ningún método EXACTO, para dividir un ángulo en 3 partes iguales o en 5 partes iguales. Los métodos existentes, son aproximados. Solamente podremos hacer la diivisión en las siguientes condiciones: Dividir un ángulo de 90º en tres partes iguales.
.
2.1.6. Otras operaciones
- Trazado de la bisectriz de un ángulo cuando el vértice queda fuera de los límites del dibujo.
- Trazar una recta que pase por un punto P dado y que sea concurrente con otras dos (rectas r y s).
- Bisectriz de un ángulo curvilíneo.
- Bisectriz de un ángulo mixtilíneo.
.