3.1.1. Tiángulos. Elementos notables

Los elementos notables de los triángulos se componen de rectas con unas características especiales y de los puntos generados por dichas rectas.

Rectas notables. Las rectas notables del triángulo son:

• Mediana.
• Bisectriz.
• Altura.
• Mediatriz.

Puntos notables. Los puntos notables son aquellos que se generan a partir de la intersección de cada una de estas rectas notables. Los puntos notables son:

• Baricentro. Formado por la intersección de las tres medianas de un triángulo.
• Incentro. Formado por la intersección de las tres bisectrices de un triángulo.
• Ortocentro. Formado por la intersección de las tres alturas de un triángulo.
• Circucentro. Formado por la intersección de las tres mediatrices de un triángulo.

Distribución:

1. Mediana – Baricentro.
2. Bisectriz – Incentro.
3. Altura – Ortocentro.
4. Mediatriz – Circucentro.

3.1.2.1. Mediana – Baricentro

La MEDIANA es la recta que une uno de los vértices con el punto medio del lado opuesto.

Habrá que hayar el punto medio del lado a (Ma) y unirlo con el vértice A. De la misma forma, hayamos los puntos medios de los lados b y c (Mb y Mc) y unirlos con los vértices B y C. La unión de las tres medianas se cortan en el punto llamado BARICENTRO.

.

3.1.2.2. Bisectriz – Incentro

La BISECTRIZ es la recta que divide el ángulo (de los vértices) en dos partes iguales. Alargando las bisectrices de los tres ángulos, se cortan en un punto llamado INCENTRO.

Habrá que trazar las bisectrices de los ángulos de los vértices. Lo puedes recordar en el siguiente enlace; ¿como se traza una BISECTRIZ?.

Las bisectrices de los tres ángulos, bisectriz de A, bisectriz de B y bisectriz de C, se cortan en un punto llamado INCENTRO.

El incentro de un triángulo

• es el centro de la circunferencia inscrita en el propio triángulo y, por lo tanto,
• equidista de sus tres lados,
• siendo tangente a los lados.

.

3.1.2.3. Altura – Ortocentro

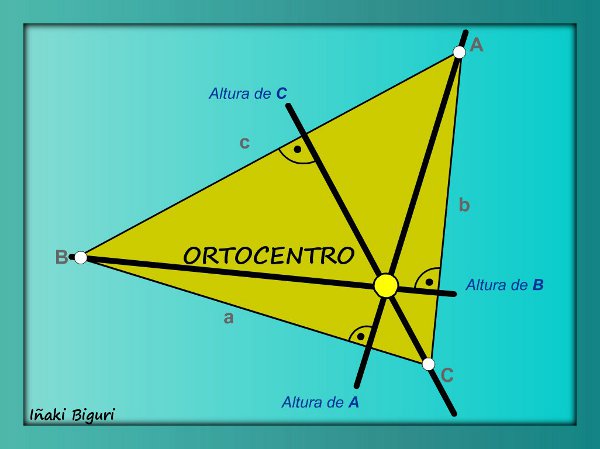
La ALTURA es la recta que va desde un vértice a su lado opuesto, de forma perpendicular. Es decir, las tres alturas de un triángulo deberán ser perpendiculares a cada uno de los lados y además deberán pasar por su vértice opuesto.

El punto de intersección de las tres alturas de un triángulo, se llama ORTOCENTRO. + Detalle

.

3.1.2.4. Mediatriz – Circucentro

La MEDIATRIZ es la recta que divide un segmento en dos partes iguales. En un triángulo, las mediatrices son las líneas que dividen los lados del triángulo en dos partes iguales.

Habrá que trazar las mediatrices de los lados de los ángulos. Lo puedes recordar en el siguiente enlace; ¿como se traza una MEDIATRIZ?.

Las mediatrices de los lados del triángulo, se cortan en un punto llamado CIRCUCENTRO.

El circucentro de un triángulo

• es el centro de la circunferencia circunscrita en el propio triángulo y, por lo tanto,
• pasa por todos los vértices del triángulo,
• teniendo todos los puntos del triángulo, dentro de la circunferencia.