 Un Romboide es un cuadrilátero, o sea, un polígono, que tiene los lados iguales dos a dos y sus ángulos también iguales dos a dos, pero distintos del ángulo recto.
Un Romboide es un cuadrilátero, o sea, un polígono, que tiene los lados iguales dos a dos y sus ángulos también iguales dos a dos, pero distintos del ángulo recto.
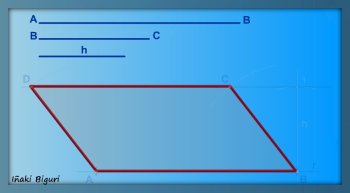
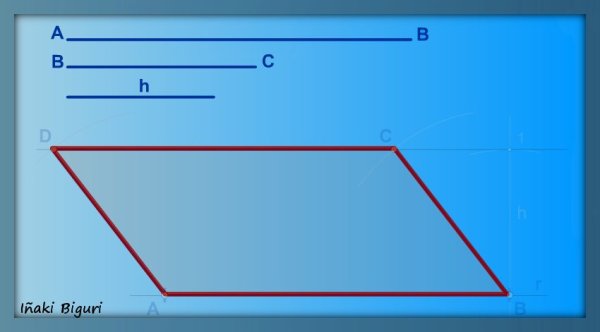
Se trata de construir un Romboide conociendo los lados paralelos y la altura.
.

.
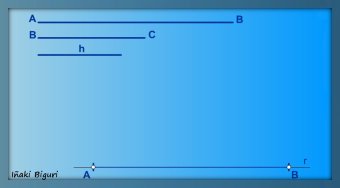
1. Sobre una recta r cualquiera, colocamos el lado mayor del romboide, que viene determinado por el segmento AB.
.
.
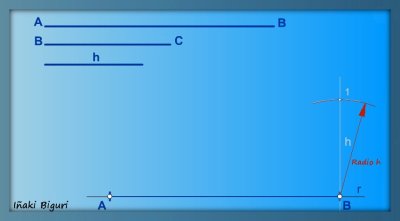
2. Sabemos que la altura se representa sobre una perpendicular a la base, por lo tanto, en uno de los dos extremos del segmento, por ejemplo el punto B, trazamos (con ayuda de la escuadra y el cartabón) una perpendicular a r
Sobre esta perpendicular y, utilizando un compás, llevamos la medida de la altura. Obtenemos el punto 1.
.
.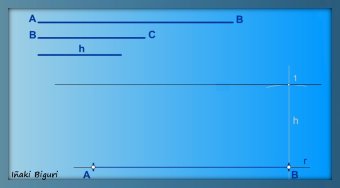
3. Por el punto 1, trazamos (con ayuda de la escuadra y el cartabón) una paralela a la recta r (o bien al segmento AB).
.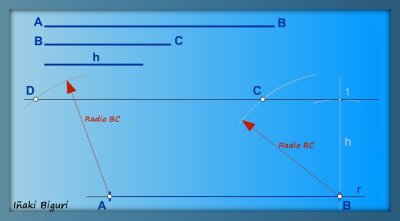
4. Desde los puntos A y B, se trazan sendos arcos con la medida del compás equivalente al segundo lado (lado BC) del romboide.
Con el arco trazado desde punto B, obtenemos el punto C; y desde el punto A, obtenemos el punto D.
.
.
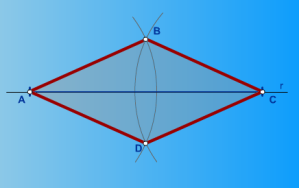
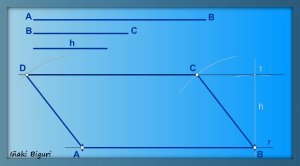
5. Se unen todos los puntos A, B, C y D y obtenemos el Romboide.
.
.
6. Se repasan todos los lados (puntos A, B, C y D) para finalizar el trabajo.
.
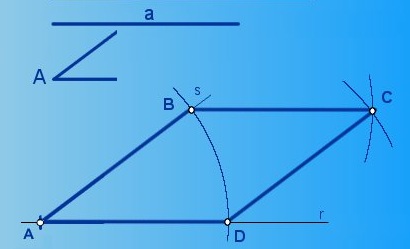
Resumen en imágenes
.



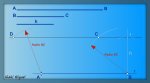
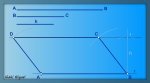
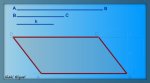



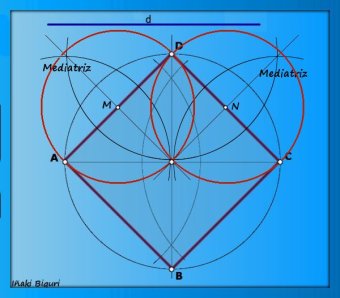
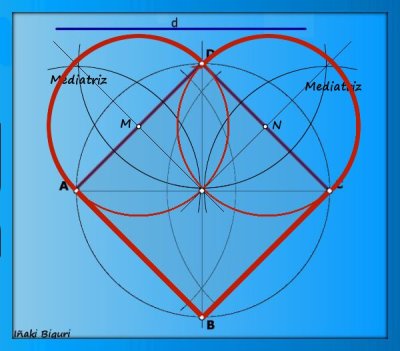

 POLÍGONOS ESTRELLADOS. Son polígonos que tienen sus ángulos salientes y entrantes de forma alternativa, y cuyos lados constituyen una línea quebrada continua y cerrada.
POLÍGONOS ESTRELLADOS. Son polígonos que tienen sus ángulos salientes y entrantes de forma alternativa, y cuyos lados constituyen una línea quebrada continua y cerrada.





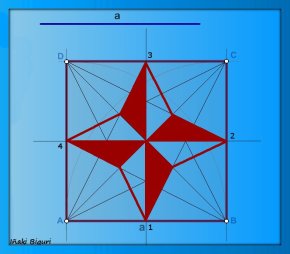
 Un
Un 
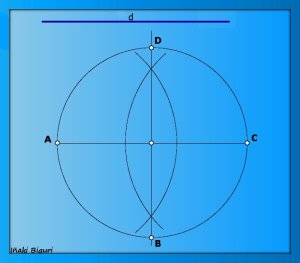


 Un
Un 









 Sobre el punto A,
Sobre el punto A, 
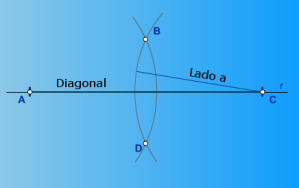
 Se coloca la diagonal sobre una recta r cualquiera. Se obtienen los puntos A y C
Se coloca la diagonal sobre una recta r cualquiera. Se obtienen los puntos A y C