 En el moviliario popular vasco, existe una gran tradición de decorar con distintos tipos de estrellas. Las podemos encontrar en estanterías, mesas, sillas, arcas, puertas, etc.
En el moviliario popular vasco, existe una gran tradición de decorar con distintos tipos de estrellas. Las podemos encontrar en estanterías, mesas, sillas, arcas, puertas, etc.
En la imagen, tenemos una silla decorada con una estrella de 8 puntas. Veamos cómo se hace.
POLÍGONOS ESTRELLADOS. Son polígonos que tienen sus ángulos salientes y entrantes de forma alternativa, y cuyos lados constituyen una línea quebrada continua y cerrada.
Los polígonos regulares estrellados son aquellos que tienen todos sus lados y ángulos iguales.
Ya vimos como trabajar un octógono estrellado, pero en aquella ocasión buscábamos una estrella de 4 puntas. En este caso veremos que, el octógono regular estrellado, también llamado polígono estrellado de 8 puntas, se construye de la siguiente forma:
OPERACIONES
 1. Partimos con el octógono inscrito que hicimos en un trabajo anterior.
1. Partimos con el octógono inscrito que hicimos en un trabajo anterior.
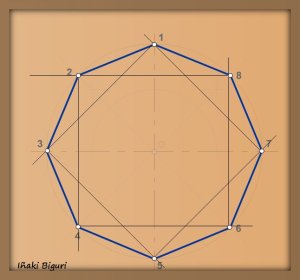
Según se explicó en el tema en 3.5. Polígonos estrellados, el octógono me dará dos posibles soluciones, es decir dos estrellas distintas.
.
2. Para la primera, utilizaremos un avance 2, esto es, uniendo los vértices cada dos.
Unimos el vértice 1, con el 3. De la misma manera, unimos el vértice 2, con el 4, el 3 con el 5… y continuamos este procedimiento hasta completar todos los vértices.
Esta operación se deberá realizar con un trazo fino del lápiz (2H), para no emborronar el dibujo.
.
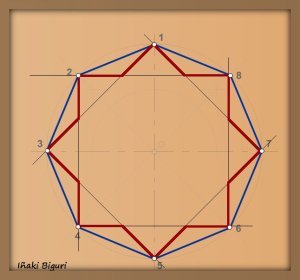
3. Para dar por acabado el trabajo, habrá que repasar, con un trazo grueso del lapiz (2B), los vértices que queremos conservar, dejando sin marcar (si el trazado es fino, no será necesario borrar) los trazos que no me interesan.
 Conseguimos la primera estrella de 8 puntas.
Conseguimos la primera estrella de 8 puntas.
Solución 1.
 4. Para la segunda estrella, utilizaremos un avance 3, es decir uniremos los vértices cada tres.
4. Para la segunda estrella, utilizaremos un avance 3, es decir uniremos los vértices cada tres.
Igual que en el caso anterior, unimos el vértice 1, con el 4, el vértice 2, con el 5, el 3 con el 6… y continuamos este procedimiento hasta completar todos los vértices.
En esta operación se utilizará un trazo fino del lápiz (2H), para no emborronar el dibujo.
 .
.
5. Repasaremos, con un trazo grueso del lapiz (2B), los vértices que queremos conservar, dejando sin marcar (si el trazado es fino, no será necesario borrar) los trazos que no me interesan.
Vemos que esta estrella se va pareciendo a la de la silla del inicio.
 Conseguimos la segunda estrella de 8 puntas.
Conseguimos la segunda estrella de 8 puntas.
Solución 2.
.
 6. Uniendo el centro del octógono con cada uno de los vértices de la estrella, los cóncavos y los convexos, tendremos que cada punta está formada por un rombo.
6. Uniendo el centro del octógono con cada uno de los vértices de la estrella, los cóncavos y los convexos, tendremos que cada punta está formada por un rombo.
Cuando sombreamos todas las mitades de ese rombo, obtenemos una estrella con aspecto tridimensional.
En este caso, nuestra estrella de 8 puntas dibujada sobre el papel, se parece totalmente a la imagen de la estrella de la silla.


.
.
 Esto ya lo vimos en las construcciones:
Esto ya lo vimos en las construcciones:


 3.
3.  Ya hemos conseguido encontrar el valor del lado del equilátero.
Ya hemos conseguido encontrar el valor del lado del equilátero.
 Los dos arcos trazados anteriormente, se cortan en un punto A, que será el vértice superior del triángulo equilátero.
Los dos arcos trazados anteriormente, se cortan en un punto A, que será el vértice superior del triángulo equilátero.
 POLÍGONOS ESTRELLADOS. Son polígonos que tienen sus ángulos salientes y entrantes de forma alternativa, y cuyos lados constituyen una línea quebrada continua y cerrada.
POLÍGONOS ESTRELLADOS. Son polígonos que tienen sus ángulos salientes y entrantes de forma alternativa, y cuyos lados constituyen una línea quebrada continua y cerrada.








 Como ya se ha dicho en otra ocasión, para construir un triángulo necesitamos tres datos.
Como ya se ha dicho en otra ocasión, para construir un triángulo necesitamos tres datos.


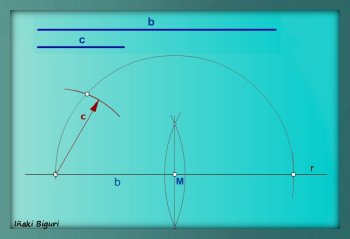
 Según lo dicho anteriormente, si unimos este punto con los dos extremos de la hipotenusa b, obtenemos un triángulo rectángulo.
Según lo dicho anteriormente, si unimos este punto con los dos extremos de la hipotenusa b, obtenemos un triángulo rectángulo.






 En otra ocasión vimos la
En otra ocasión vimos la 




 .
.










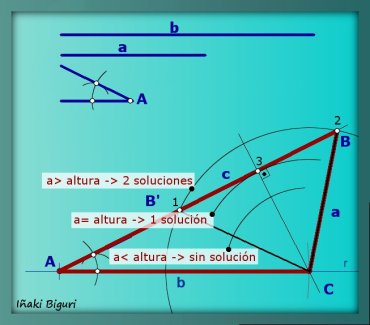

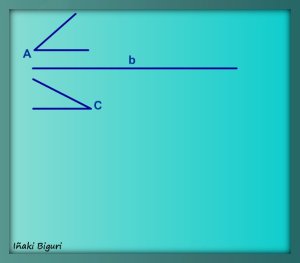 Ángulos adyacentes son los que tienen un vértice y un lado comun. En nuestro caso tenemos que el lado b, es el lado común a los dos ángulos A y C. A partir de este dato, el ejercicio es sencillo.
Ángulos adyacentes son los que tienen un vértice y un lado comun. En nuestro caso tenemos que el lado b, es el lado común a los dos ángulos A y C. A partir de este dato, el ejercicio es sencillo.

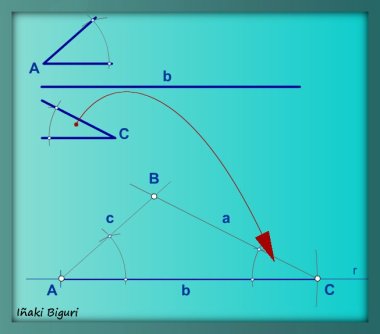
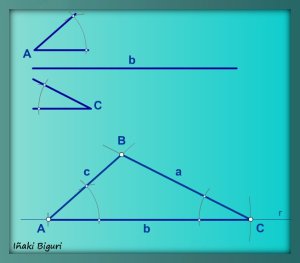
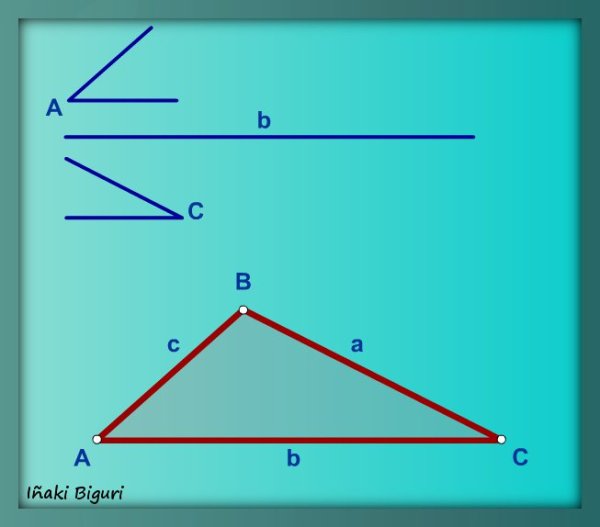
 Este ejercicio se puede realizar de varias formas, pero para resolverlo utilizaremos
Este ejercicio se puede realizar de varias formas, pero para resolverlo utilizaremos 




