
Pieza 605
Nos dan la pieza de la figura (pieza 605) y nos piden delinearla.
Para ello tenemos que sacar las vistas que representen esta pieza. Delinear es obtener esas mismas vistas pero utilizando las herramientas de dibujo y las medidas que me proporciona la pieza.

 Aunque la obtención de vistas (alzado, planta y perfil) no es objeto de este blog, podemos ver que no tiene excesiva complicación.
Aunque la obtención de vistas (alzado, planta y perfil) no es objeto de este blog, podemos ver que no tiene excesiva complicación.
.
Las vistas serían:
.
Nos fijamos en que hay que realizar enlaces en el perfil.
En este caso, el enlace consiste en unir dos rectas paralelas del perfil con un arco semicircular (ejemplo: enlazar dos líneas paralelas).
Enlazar dos rectas
Para hacer cualquier enlace hay que realizar tres operaciones:
- Hallar el centro del enlace
- Hallar los puntos de tangencia
- Trazar el enlace (primero el arco y luego las rectas)
Para hallar el centro del enlace, lo podemos hacer matemáticamente o gráficamente. Dado que estamos trabajando la interpretación gráfica, lo haremos gráficamente y mediante el trazado de la mediatriz.
La mediatriz es la línea que divide un segmento en dos partes iguales.
Dicho de otra forma, si queremos dividir un segmento (trozo de una línea, limitado en sus dos extremos) en dos partes iguales, tendremos que utilizar la mediatriz.
Mediatriz
 Para trazar una mediatriz, se coge el compás y con una abertura cualquiera, más grande que la mitad del segmento, se traza un arco desde uno de los dos puntos, por ejemplo el punto A.
Para trazar una mediatriz, se coge el compás y con una abertura cualquiera, más grande que la mitad del segmento, se traza un arco desde uno de los dos puntos, por ejemplo el punto A.
Después, y con el mismo radio anterior, se traza otro arco desde el punto B.
Ambos arcos se cortan en los puntos 1 y 2. Juntando estos dos puntos, tendremos la MEDIATRIZ.
El punto medio del segmento AB, es donde la mediatriz corta al segmento. Este es el centro del enlace.
Aplicación en la pieza. Centro del enlace
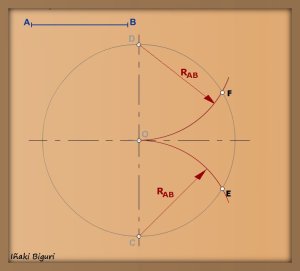
 En nuestra pieza, sería:
En nuestra pieza, sería:
.
La altura donde se sitúa el eje horizontal, se obtiene de las medidas de la perspectiva de la pieza.
Aprovechamos el trazado y marcamos el eje horizontal con línea de eje (trazos y puntos).
.
 .
.
Como hemos visto antes, desde los extremos, trazamos dos arcos con un radio del compás algo mayor de la mitad del segmento.
Uniendo la intersección de estos dos arcos, tenemos el punto Oe, que es la mitad del segmento y por tanto el punto desde donde tendremos que hacer el enlace.
Aprovechamos el trazado y marcamos el eje vertical.
Puntos de tangencia
 Después de tener el centro del enlace, tenemos que saber cuales son los puntos de tangencia.
Después de tener el centro del enlace, tenemos que saber cuales son los puntos de tangencia.
.
Este caso es sencillo ya que, donde el eje horizontal corta a las aristas del perfil, tenemos los puntos de tangencia T1 y T2.
.
Trazado del enlace
 Con los puntos de tangencia hallados, trazamos el arco del enlace.
Con los puntos de tangencia hallados, trazamos el arco del enlace.
El enlace unirá los puntos de tangencia (saldrá del punto de tangencia 1 y finalizará en el punto de tangencia 2). Primero en fino, para ver si está bien realizado, y luego en grueso.
Aprovechando este trazado, realizamos de la misma manera (primero en fino y luego en grueso) el círculo correspondiente al agujero que tiene el perfil.
 .
.
Para finalizar se trazan, con línea gruesa, el resto de líneas correspondientes al perfil.
Quedará de la siguiente manera:
.
.
.
Tipos de líneas y sus grosores
Además, nos fijamos en las líneas y sus grosores. Según se comenta en el apartado «líneas normalizadas«, las líneas tienen unas características diferenciadas de trazado y de dimensión, dependiendo de su función.
En el apartado de tipo de líneas y aplicaciones, podemos ver:
- Línea continua o línea gruesa. Utilizada en contornos vistos y aristas vistas. De los tres tipos de línea es la más gruesa. Se dibujará con el lápiz 2B.
- Línea discontinua. Utilizada en contornos ocultos y aristas ocultas. Son de grosor medio, para diferenciarlo de las líneas continuas. De los tres tipos de línea es la más gruesa. Se dibujará con el lápiz 2B.
- Línea de trazos y puntos. Se trata de una línea fina, la más fina de todas, formada de trazos y puntos. Se utiliza en ejes de revolución, ejes de simetría y trayectorias.
Veamos un ejemplo:

Finalización de la lámina
Después de realizar el enlace y de repasar todas las líneas con el tipo de lápiz (según los grosores vistos anteriormente) adecuado a cada línea, las vistas delineadas quedarían así:


- Siempre que tengamos partes circulares en una pieza, vamos a tener que realizar algún tipo de enlace del tipo curva-recta o curva-curva.
- Los enlaces se deben hacer siguiendo unos pasos:
- Hallar el centro del enlace
- Hallar los puntos de tangencia
- Trazar el enlace
- El enlace unirá los puntos de tangencia (saldrá del punto de tangencia 1 y finalizará en el punto de tangencia 2.
- Existe series de tres tipos de grosores (grueso, medio y fino) que debemos tener en cuenta para el trazado final de la pieza.
- Se debe apreciar fácilmente la diferencia entre los tipos de línea mediante la utilización de los grosores de línea.
 Un rombo, como se ve en el apartado «cuadriláteros«, es un cuadrilátero (figura plana formada por cuatro lados que se cortan dos a dos) además de un Paralelogramo (por tener sus lados paralelos dos a dos).
Un rombo, como se ve en el apartado «cuadriláteros«, es un cuadrilátero (figura plana formada por cuatro lados que se cortan dos a dos) además de un Paralelogramo (por tener sus lados paralelos dos a dos).




 Aunque la obtención de vistas (alzado, planta y perfil) no es objeto de este blog, podemos ver que no tiene excesiva complicación.
Aunque la obtención de vistas (alzado, planta y perfil) no es objeto de este blog, podemos ver que no tiene excesiva complicación. Para trazar una mediatriz, se coge el compás y con una abertura cualquiera, más grande que la mitad del segmento, se traza un arco desde uno de los dos puntos, por ejemplo el punto A.
Para trazar una mediatriz, se coge el compás y con una abertura cualquiera, más grande que la mitad del segmento, se traza un arco desde uno de los dos puntos, por ejemplo el punto A. En nuestra pieza, sería:
En nuestra pieza, sería:
 Después de tener el centro del enlace, tenemos que saber cuales son los puntos de tangencia.
Después de tener el centro del enlace, tenemos que saber cuales son los puntos de tangencia. Con los puntos de tangencia hallados, trazamos el arco del enlace.
Con los puntos de tangencia hallados, trazamos el arco del enlace.



 estudios que les cualificarán para acceder a un puesto de trabajo con garantias de empleabilidad.
estudios que les cualificarán para acceder a un puesto de trabajo con garantias de empleabilidad.


 En el moviliario popular vasco, existe una gran tradición de decorar con distintos tipos de estrellas. Las podemos encontrar en estanterías, mesas, sillas, arcas, puertas, etc.
En el moviliario popular vasco, existe una gran tradición de decorar con distintos tipos de estrellas. Las podemos encontrar en estanterías, mesas, sillas, arcas, puertas, etc. 1.
1. 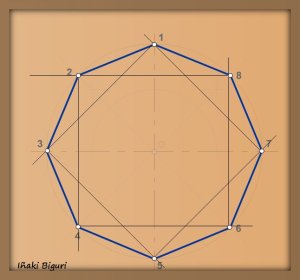
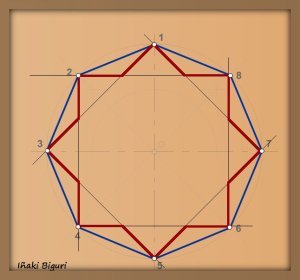
 Conseguimos la primera estrella de 8 puntas.
Conseguimos la primera estrella de 8 puntas.
 .
. Conseguimos la segunda estrella de 8 puntas.
Conseguimos la segunda estrella de 8 puntas. 6.
6.

 Esto ya lo vimos en las construcciones:
Esto ya lo vimos en las construcciones:


 3.
3.  Ya hemos conseguido encontrar el valor del lado del equilátero.
Ya hemos conseguido encontrar el valor del lado del equilátero.
 Los dos arcos trazados anteriormente, se cortan en un punto A, que será el vértice superior del triángulo equilátero.
Los dos arcos trazados anteriormente, se cortan en un punto A, que será el vértice superior del triángulo equilátero.

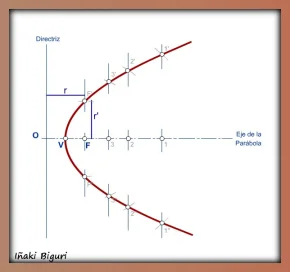



 Trazamos arcos desde el foco F con los radios: RO2, RO3 y ROF.
Trazamos arcos desde el foco F con los radios: RO2, RO3 y ROF.
 POLÍGONOS ESTRELLADOS. Son polígonos que tienen sus ángulos salientes y entrantes de forma alternativa, y cuyos lados constituyen una línea quebrada continua y cerrada.
POLÍGONOS ESTRELLADOS. Son polígonos que tienen sus ángulos salientes y entrantes de forma alternativa, y cuyos lados constituyen una línea quebrada continua y cerrada.








 En otra ocasión vimos la
En otra ocasión vimos la 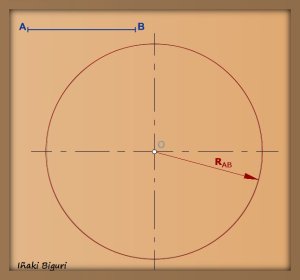
 .
.
 4.
4.
 Como en otras ocasiones, debemos aconsejar el trazar los arcos desde un lado del eje vértical (lado izquierdo: vértices 2, 3, 4, y 5) y desde el otro (lado derecho: vértices 9, 8, 7 y 6). De esta forma, estaremos repatartiendo el posible error.
Como en otras ocasiones, debemos aconsejar el trazar los arcos desde un lado del eje vértical (lado izquierdo: vértices 2, 3, 4, y 5) y desde el otro (lado derecho: vértices 9, 8, 7 y 6). De esta forma, estaremos repatartiendo el posible error.

 Este ejercicio se podría haber realizado matemáticamente: con un
Este ejercicio se podría haber realizado matemáticamente: con un 
 En nuestro caso cogemos una abertura del compás de radio R, y trazamos arcos en los tres ángulos y en el punto O de la recta r. Insisto, la abertura del compás puede ser cualquiera, pero una vez elegida, no se puede modificar y se trazará en todos los ángulos y el punto O.
En nuestro caso cogemos una abertura del compás de radio R, y trazamos arcos en los tres ángulos y en el punto O de la recta r. Insisto, la abertura del compás puede ser cualquiera, pero una vez elegida, no se puede modificar y se trazará en todos los ángulos y el punto O. 3.
3.


